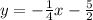Answer:
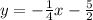
Explanation:
Point-Slope Form:
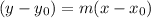 where
where
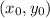 is the point our line is passing through and
is the point our line is passing through and
 is the slope of our line.
is the slope of our line.
The question asks us for an equation parallel to
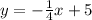 .
.
We identify that the equation provided is in y-intercept form:

A line parallel to
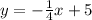 will have the same slope.
will have the same slope.
Thus,
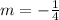 .
.
We were provided the point
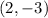 .
.
Plugging into our equation for point-slope form:

This is our answer, however we can simplify this equation into y-intercept form by simply solving for y:
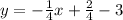
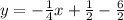
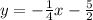
Thus, the equation parallel to
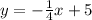 passing through
passing through
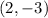 is:
is: