Question

HELP ASAP!!!!! Given: Point B is on the perpendicular bisector of AC¯¯¯¯¯. BD¯¯¯¯¯ bisects AC¯¯¯¯¯ at point D. Prove: B is equidistant from A and C. An isosceles triangle A B C. Point D lies on side A C. An altitude is drawn from point B to point D. What are the missing parts that correctly complete the proof?

Answer 1

Answer: Missing parts are,

In first blank,
`AD\cong DC`,

In second blank, SAS postulate

In third blank, CPCTC postulate

Explanation:

Since, Here D is the mid point on the line segment AC.

And BD is a perpendicular to the line AC.

Therefore, In triangles ADB and CDB ( shown in figure)

AD\cong DC ( By the definition of mid point)

`\angle BDA\cong \angle BDC` ( right angles )

`BD\cong BD` ( reflexive)

Thus, By SAS ( side angle side )postulate,

`\triangle ADB\cong \triangle CDB`

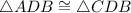
So, by CPCTC( Corresponding parts of congruent triangles are congruent)

`AB\cong CB`

Now, By definition of congruent segment,

AB=CB

By definition of equidistant,

B is equally far from both A and C.

Answer 2

Point B is on the perpendicular bisector of AC. BD bisects Ac at point D.

Given.

AD ≅ DC Definition of bisector.

<ADB and <CDB are right angles Definition of perpendicular.

<ADB = <CDB All right angles are congruent.

BD = BD Reflexive property.

Triangle △ADB ≅ △CDB SAS congruence Postulate.

AB = CB CPCTC

AB = CB Definition of congruent segments

B is equidistant from A and C Definition of equidistant.