Question

The greater of is 7 more than the lesser. three times the greater number is 5 more than r4 times the lesser number. Find the numbers

Answer 1

Steps:

(Let x = greater number and y = lesser number)

So this question is asking us for a system of equations. Using the info they provide, we can form these two equations:

`x=y+7\ \textsf{(`

So for this, we will be using the substitution method. Since we know that x = y + 7, substitute x with (y + 7) in the second equation as such:

`3(y+7)=4y+5`

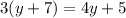
From here we can solve for y. Firstly, distribute 3 so that it multiplies with y and 7:

`3y+21=4y+5`

Next, subtract 3y on both sides of the equation:

`21=y+5`

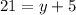
Lastly, subtract 5 on both sides of the equation:

`16=y`

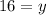
Now that we know the value of y, we can substitute it into either equation to solve for x:

`x=16+7\\x=23\\\\3x=4(16)+5\\3x=64+5\\3x=69\\x=23`

Answer:

In short, 16 is the lesser number and 23 is the greater number.