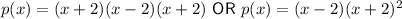Question

P(x)=x^3+2x^2-4x-8 how do you factor this polynomial function

Answer 1

Steps:

So for this, I will be factoring by grouping. Firstly, factor x³ + 2x² and -4x - 8 separately. Make sure that they have the same quantity inside of the parentheses:

`p(x)=x^2(x+2)-4(x+2)`

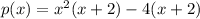
Now we can rewrite it as:

`p(x)=(x^2-4)(x+2)`

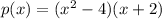
However, we aren't finished factoring yet. The first factor, x² - 4, can be factored further using the difference of squares. The difference of squares goes by the formula here:
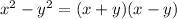`x^2-y^2=(x+y)(x-y)` . In this case:

`x^2-4=(x+2)(x-2)\\p(x)=(x+2)(x-2)(x+2)`

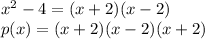
Answer:

In short, the answer is
`p(x)=(x+2)(x-2)(x+2)\ \textsf{OR}\ p(x)=(x-2)(x+2)^2`