Answer:
The numerator has two terms.
The denominator has three terms.
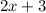 is a single factor in the numerator.
is a single factor in the numerator.
Explanation:
We have the following rational expression :

In which
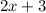 is the numerator and
is the numerator and
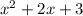 is the denominator
is the denominator
In any mathematical expression the symbols ''+'' and ''-'' divide the expression into terms. For example :
 has three terms :
has three terms :
1 , 2 and 3
For a polynomial P(x) a factor is any polinomial which divides evenly into P(x).
For example :

This means that If we divide
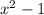 by
by
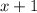 we obtain
we obtain
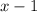
If we divide
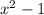 by
by
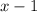 we obtain
we obtain
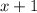
We conclude that
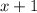 and
and
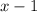 are factors of the expression
are factors of the expression
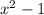 . The expression
. The expression
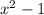 has two factors.
has two factors.
Let's evaluate the statements for this rational expression.
The numerator has two terms. This is actually true. The terms are
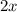 and
and
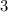
The denominator has three factors. This is wrong. The degree of the denominator is two .This means that it can have at most two factors (real or imaginary).
The denominator has three terms. This is true. The terms are
 ,
,
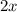 and
and
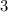
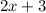 is a single factor in the numerator. This is true because we can write the following expression :
is a single factor in the numerator. This is true because we can write the following expression :
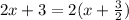 and the expression
and the expression
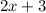 will be a single factor.
will be a single factor.
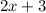 in the numerator divides out with
in the numerator divides out with
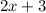 in the denominator. This is wrong. We can't forget about
in the denominator. This is wrong. We can't forget about
 in the denominator If we want to make the division.
in the denominator If we want to make the division.