Question

Water flowing through a garden hose of diameter 2.74cm fills a25.0L bucket in 1.50 min a) what is the speed of the water leaving the end of the hose? B)a nozzle is now attached to the end of the hose.if the nozzle diameter is one third the diameter of the hose, what is the speed of the water leaving the nozzle?

Answer 1

(a) The speed of water leaving the hose is 0.471 m/s

(b) The speed of water leaving the nozzle is 4.24 m/s.

(a) Let the area of the hose be a₁ and the speed water leaving the hose be v₁. In 1 second, the volume of water flowing per second
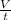`(V)/(t)` is given by,

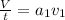`(V)/(t) =a_1v_1` ......(1)

The volume of the bucket is
`V=25.0 *10^-^3m^3`

The radius of the hose is
`r_1=(2.74*10^-^2 m)/(2) =1.37*10^-^2 m`

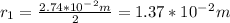
From equation (1),

`v_1=(V)/(A_1t) =(V)/(\pi r_1^2t)`

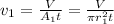
Substitute the given values in the equation.

`v_1 =(V)/(\pi r_1^2t)\\ =(25.0*10^-^3m^3)/((1.50*60s)(3.14)(1.37*10^-^2)^2) \\ =0.471 m/s`

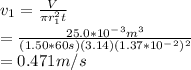
(b) A nozzle is now attached to the hose. The volume of liquid which flows out per second through the hose and the nozzle remains the same. If the area of the nozzle is a₂ and the speed at which the water exits the nozzle is v₂, then,

`a_1v_1=a_2v_2\\ v_2=(a_1)/(a_2) v_1`

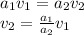
If the diameter of the nozzle is one third of the diameter of the hose, then,since area is directly proportional to the square of the diameter,

`(a_1)/(a_2) =9`

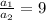
Therefore,

`v_2=(a_1)/(a_2) v_1\\ =9*0.471m/s\\ =4.24m/s`

Thus, the speed of water leaving the hose is 0.471 m/s and the speed of water leaving the nozzle is 4.24 m/s.

Answer 2

a) Speed of the water leaving the end of the hose = 0.47 m/s

b) Speed of the water leaving the end of the nozzle = 4.25 m/s

Step-by-step explanation:

Discharge, Q = Av , where A is the area discharging section and v is the velocity of flow.

Volume of bucket = 25.0 L

Time taken = 1.50 min

Discharge = Volume / Time = 25/1.5 = 16.67 L/min.

`=(16.67*10^(-3))/(60) =2.78*10^(-4) m^3/s`

a) Diameter of hose = 2.74 cm = 0.0274 m

Q = Av

`2.78*10^(-4)=\frac{\pi*0.0274^2} {4} *v\\ \\ v=0.47m/s`

Speed of the water leaving the end of the hose = 0.47 m/s

b) Diameter of nozzle = Diameter of hose/3 = 0.0274/3 = 0.00913 m

Q = Av

`2.78*10^(-4)=\frac{\pi*0.00913^2} {4} *v\\ \\ v=4.25m/s`

Speed of the water leaving the end of the nozzle = 4.25 m/s