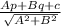To Find: Distance between point P to line l
Solution: Points lying on line l are suppose A (-4,2) and B (3,-5).
Equation of line passing through (p,q) and (a,b) is given by the equation
→
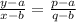
Equation of line AB is ,
→
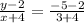
→y -2 = -1× (x +4)
→y -2 = -x -4
→x + y +4-2=0
→ x + y +2=0
Distance between point P (1,2) and line l whose equation is ,x+y+2=0 is given by=
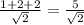 =5√2/2=3.535(approx)→Option (C)
=5√2/2=3.535(approx)→Option (C)
→Which is given by the formula ,i.e if a line has equation , Ax + By +c=0 and we have to find the distance from (p,q) is given by =