Answer-
He must use 75 pound of first kind and 25 pound of second kind tea.
Solution-
Price of first kind tea per pound = $0.32
Price of second kind tea per pound = $0.40
By selling it at $0.43 per pound he made a profit of 25%
Let the cost price is x, then
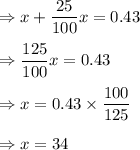
The cost price of the mixed kind is $0.34
Then, let the amount of first kind tea in the 100 pound mixture is y pound, so the amount of second kind tea is (100-y) pound
So, the price of mixture will be equal to the sum of price of each kind,
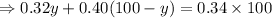
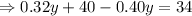
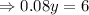


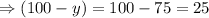
Therefore, he must use 75 pound of first kind and 25 pound of second kind tea.