Answer : D
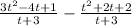
The denominators are same
So we combine the numerators
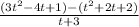
To remove parenthesis we distribute negative sign inside the second parenthesis
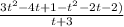
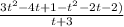
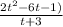
Morgan made a mistake. He forgot to distribute the negative sign
Morgan forgot to distribute the negative sign to two of the terms 2t and 2 inside second parenthesis