Answer:

Step-by-step explanation (using the Unit Circle):
csc
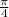 - cos
- cos

csc =
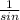
sin
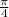 =
=
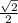
→ csc
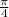 =
=
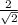 =
=
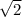
cos
 =
=

csc
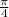 - cos
- cos

=
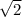 -
-

=
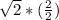 -
-

=
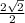 -
-

=

Step-by-step explanation (using the special triangles):
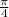 = 45°
= 45°
a 45°-45°-90° triangle has sides with proportions of: 1 - 1 - √2
csc =
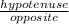 =
=
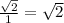
 = 30°
= 30°
a 30°-60°-90° triangle has sides with proportions of: 1 - √3 - 2
cos =
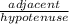 =
=

csc
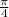 - cos
- cos
 =
=
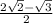
*****************************************************************************************
Answer: secθ
Explanation:
cosθ csc²θ tan²θ
= cosθ *
 *
*
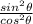
=
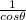
= secθ