Question

University administrators have developed a Markov model to simulate graduation rates at their school. Students might drop out, repeat a year, or move on to the next year. Students have a 3% chance of repeating the year. First-years and sophomores have a 6% chance of dropping out. For juniors and seniors, the drop-out rate is 4%. Compute the probability that a student who starts as a 1st-year eventually graduates the university.

Answer 1

The percentage of the students who have a chance of repeating their current year = 3%

The drop out students for the first year and the sophomores = 6%

Drop out rate of first year and the seniors = 4%

Now for the state space :

S = { first year(1), sophomores(2), juniors(3), seniors(4), graduates(G), Dropouts(D) }

Therefore

the first year students are indicated as '1'

Sophomores are indicated as '2'

Juniors are indicated as '3'

Seniors are indicated as '4

Graduates are indicated as 'G'

Dropouts are indicated as 'D'

The transition diagram is attached below.

The probability of the students who have the chance of repeating their current year = 3/100 = 0.03

Probability of first year dropouts and sophomores = 6/100 = 0.06

Probability of dropout rate of juniors and seniors = 4/100 = 0.04

Therefore, the probability matrix can be made as :

1 2 3 4 G D

`\begin{matrix}1\\ 2\\ 3\\ 4\\ G\\ D\end{matrix}`
`\begin{bmatrix}0.03 & 0.91 & 0 & 0 & 0 & 0.06\\ 0& 0.03 & 0.91 & 0 & 0 & 0.06\\ 0& 0 & 0.03 & 0.93 & 0 & 0.04\\ 0& 0 & 0 & 0.03 & 0.93 & 0.04\\ 0& 0 & 0 & 0 & 1 & 0\\ 0& 0 & 0 & 0 & 0 & 1\end{bmatrix}`

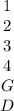
Here, G represents 'graduates' and D represents 'Dropouts.'