Question

Mr. Callahan hung up two mirrors. Each mirror was centered over each sink in the bathroom vanity as shown below. The vanity is centered on the wall. The wall is 11-1/4 feet long. Each mirror is 30 inches wide. The mirrors are hung 3 feet apart. What is the distance between the edge of the wall and the edge of each mirror?

Answer 1

To find the distance between the edge of the wall and the edge of each mirror, subtract the combined width of the two mirrors and the distance between them from the total width of the wall. The distance is 51 inches.

Step-by-step explanation:

To find the distance between the edge of the wall and the edge of each mirror, we need to subtract the combined width of the two mirrors and the distance between them from the total width of the wall. Here's how:

1. Calculate the total width of the two mirrors: 30 inches + 30 inches = 60 inches.
2. Calculate the total distance between the two mirrors: 3 feet * 12 inches = 36 inches.
3. Calculate the distance between the edge of the wall and the edge of each mirror: 11.25 feet * 12 inches - 60 inches - 36 inches = 51 inches.

Answer 2

We have been given that wall is
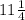`11(1)/(4)` feet long.

Let us convert it in improper fraction,

`11(1)/(4) =(45)/(4)`

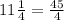
Since we know that 1 feet equals to 12 inches. Now we will convert length of wall in inches.

`12\cdot(45)/(4) =3\cdot45=135\text{ inches}`

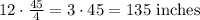
We have been given that mirrors are hung 3 feet apart that will be,

`3\cdot12=36\text{ inches}`

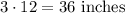
Now we will add width of both mirrors and distance between both mirrors.

`2\cdot30+36=60+36=96`

Now we will subtract 96 from 135 and divide our difference by 2 to find distance between the edge of wall and the edge of each mirror.

`(135-96)/(2) =(39)/(2)=19.5`

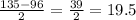
Therefore, distance between the edge of the wall and the edge of each mirror will be 19.5 inches.