Question

The product of two number is 20 and the sum of square is 41 find the number​

Answer 1

Let the two number is a and b

so,

product =ab=20

sum of square=
`\bold{a^2+b^2=41 }`

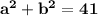
Then,

`\bold{(a+b)^2=a^2+b^2+2ab }`

`\bold{ (a+b)^2=41+2×40 }`

`\bold{ (a+b)^2=81 }`

`\bold{a+b=√(81) }`

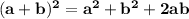
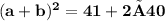
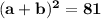
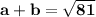
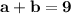`\bold{a+b=9 }`•••••••••(equation I)

Now,

`\bold{(a-b)^2=a^2+b^2-4ab }`

`\bold{ (a-b)^2=41-4×20 }`

`\bold{(a-b)^2=41-40 }`

`\bold{a-b=√(1) }`

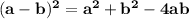
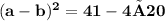
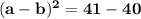
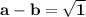
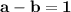`\bold{a-b=1 }`••••••••(equation II)

Now,combine the equation I and equation II

we,get

`\bold{a+b+a-b=9+1 }`

`\bold{a+\cancel{b}+a\cancel{-b}=10 }`

`\bold{ 2a=10 }`

`\bold{a=(10)/(2) }`

`\blue{\boxed{ a=5 }}`

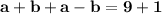
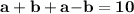
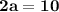
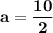
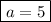
Then,

put the value of a in equation II.

we get that,

`\bold{5-b=1 }`

`\bold{b+1=5 }`

`\bold{b=5-1 }`

`\bold{\boxed{\blue{b=4}} }`

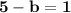
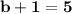
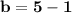
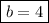
so,

The two number is 5 and 4.