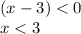Question

Rewrite the equation y=2|x−3|+5 as two linear functions f and g with restricted domains.

Answer 1

The absolute value transforms a negative number into a positive number.

For example

Let z be a real number, then:

| z | It will always be a positive number.

This means that:

If z is a negative number, then:

| z | = -z

If z is a positive number, then:

| z | = z

This means that for the expression the expression y = 2 | x-3 | +5

When
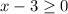`x-3 \geq 0` then:

| x-3 | = x-3

When x-3 < 0 then:

| x-3 | = - (x-3)

Then we can divide the expression into two functions f (x) and g (x).

`f(x) = 2(x-3) +5\\ f(x) = 2x-6 + 5\\ f(x) = 2x-1`

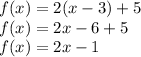
For

`x-3\geq 0\\x\geq 3`

`g(x) = 2 (-x + 3) +5\\ g(x) = -2x + 6 + 5\\ g(x) -2x +11`

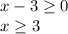
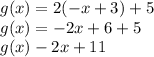
For

`(x-3) < 0\\ x < 3`