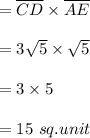Question

Find the perimeter AND area of parallelogram ABCD.

Answer 1

The perimeter and area of the parallelogram are 19.74 units and 15 sq. units respectively.

Solution-

The co-ordinates of the vertices are,

A = (-2, 3)

B = (4, 0)

C = (1, -1)

D = (-5, 2)

E = (-3, 1)

We can get the side length of the parallelogram by calculating the respective distances by applying distance formula,

`\overline{CD}=√((x_2-x_1)^2+(y_2-y_1)^2)=√((-5-1)^2+(2+1)^2)=√((-6)^2+(3)^2)=√(36+9)=√(45)=3\sqrt5`

`\overline{AD}=√((x_2-x_1)^2+(y_2-y_1)^2)=√((-2+5)^2+(3-2)^2)=√((3)^2+(1)^2)=√(9+1)=√(10)`

`\overline{AE}=√((x_2-x_1)^2+(y_2-y_1)^2)=√((-2+3)^2+(3-1)^2)=√((1)^2+(2)^2)=√(1+4)=√(5)`

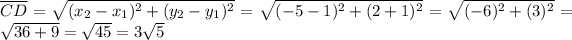
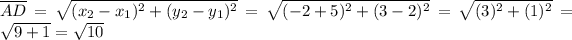
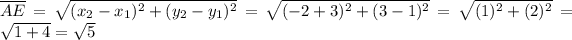
Perimeter of the parallelogram ABCD is,

`=2(\overline{AD}+\overline{CD})\\\\=2(√(10)+3\sqrt5)\\\\=19.74\ units`

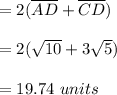
Area of the parallelogram ABCD is,

`=\overline{CD}* \overline{AE}\\\\=3\sqrt5* √(5)\\\\=3* 5\\\\=15\ sq.unit`