Answer:
The equation that represents the graph is:

Explanation:
We know that the general quadratic equation of the type:
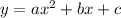
is a upward or a downward parabola depending on a.
If a>0 then the parabola is a upward open parabola.
and if a<0 then the parabola is a downward open parabola.
Hence, the option:
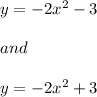
Hence, the two options are discarded as there leading coefficient is negative but the parabola is open downward.
Hence, we are left with
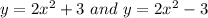
From the graph, we have when x=0 we have f(0)= -3
Hence, the only option we are left with is:

( Since, in the option:
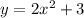 at x=0 we have y=3≠ -3 )
at x=0 we have y=3≠ -3 )