Question

The function k(x) = (g x h)(x) is graphed below, where g is an exponential function and h is a linear function. If h(x) = x + 1, which option below give the formula for g? h(^x) = 2^x

h(^x) = –2^x
h(^x) = –2^–x
h(^x) = 2^–x

Answer 1

h(x)=-2^-x, yeah this is definitely right

Answer 2

Answer: The correct option is (D)
`g(x)=2^(-x).`

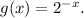
Step-by-step explanation: Given that the function k(x) = (g x h)(x) is graphed in the figure, where g is an exponential function and h is a linear function.

We are to find the formula for g, if h(x) = x + 1.

From the graph, we note the following two values :

`k(0)=1,~~k(3)=0.5.`

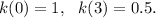
Now, will check our options one by one.

Option (A) :

Here,
`g(x)=2^x.`

S0,

`k(x)=(g* h)(x)=g(x)* h(x)=2^x(x+1).`

At x = 0 and 3, we get

`k(0)=2^0(0+1)=1,\\\\k(3)=2^3(3+1)=32\\eq 0.5.`

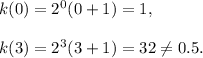
This option is not correct.

Option (B) :

Here,
`g(x)=-2^x.`

S0,

`k(x)=(g* h)(x)=g(x)* h(x)=-2^x(x+1).`

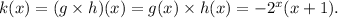
At x = 0 and 3, we get

`k(0)=-2^0(0+1)=-1\\eq 1,\\\\k(3)=-2^3(3+1)=-32\\eq 0.5.`

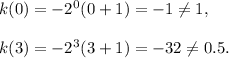
This option is not correct.

Option (C) :

Here,
`g(x)=-2^(-x).`

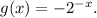
So,

`k(x)=(g* h)(x)=g(x)* h(x)=-2^(-x)(x+1).`

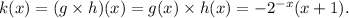
At x = 0 and 3, we get

`k(0)=-2^(-0)(0+1)=-1\\eq 1,\\\\k(3)=-2^(-3)(3+1)=-(1)/(8)(4)=-0.5\\eq 0.5.`

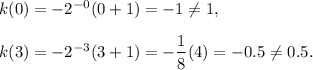
This option is not correct.

Option (D) :

Here,
`g(x)=2^(-x).`

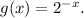
S0,

`k(x)=(g* h)(x)=g(x)* h(x)=2^(-x)(x+1).`

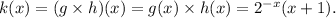
At x = 0 and 3, we get

`k(0)=2^(-0)(0+1)=1,\\\\k(3)=2^(-3)(3+1)=(1)/(8)(4)=0.5.`

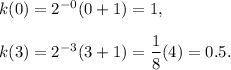
Therefore,
`g(x)=2^(-x).`

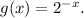
This option is CORRECT.

Hence, (D) is the correct option.