Question

99PTS!!!!!!!

You have two exponential functions. One has the formula h(x) = 3^x – 2. The other function, g(x), has the graph shown below. Which inequality below is true for all points on the indicated interval?
g(x) ≥ h(x) on the interval –2 ≤ x ≤ 2
g(x) ≥ h(x) on the interval –3 ≤ x ≤ 3
g(x) ≤ h(x) on the interval –3 ≤ x ≤ 3
g(x) ≤ h(x) on the interval –2 ≤ x ≤ 2

Answer 1

Option A.

Explanation:

The given function is

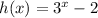`h(x)=3^x-2` ... (1)

It is an exponential function.

The graph of second exponential function passes through the points (0,4) and (1,5), and it shifted 3 units up.

`g(x)=a(b)^x+3`

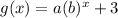
Substitute x=0 and g(x)=4 in the above function.

`4=a(b)^0+3\Rightarrow a=1`

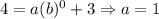
Substitute a=1, x=1 and g(x)=5 in the above function.

`5=1(b)^1+3\Rightarrow b=2`

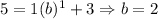
The second function is

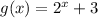`g(x)=2^x+3` .... (2)

At x=0,

`h(0)=3^(0)-2=-1`

`g(0)=2^(0)+3=4`

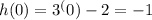
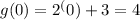
So, at initial stage g(x)>h(x).

On solving (1) and (2) we get

`x=2,g(x)=h(x)=7`

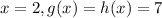
It means at x=2 the function h(x) is equal to g(x) and after that h(x)>g(x).

g(x) ≥ h(x) on the interval –2 ≤ x ≤ 2

Therefore, the correct option is A.

Answer 2

h(x) = 3^x – 2 will be negative when x is less than 0

h(2) =7

g(2)=7

This is the point they are equal

g(x)> h(x) until2

g(x)>=h(x) -2<=x<=2

Choice A