Answer:
The quadratic equation representing the area of the rectangular television screen is
 .
.
Height of the rectangular television screen
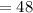 inches, and the width of the rectangular television screen
inches, and the width of the rectangular television screen
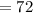 inches.
inches.
Explanation:
Given: The area of a rectangular television screen is
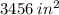 . The width of the screen is
. The width of the screen is
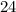 inches longer than the height.
inches longer than the height.
To find: The quadratic equation that represents the area of the screen, and what are the dimensions of the screen?
Solution:
Let the height of rectangular television screen be
 inches, then width of the rectangular screen be
inches, then width of the rectangular screen be
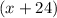 inches.
inches.
Now, we know that area of a rectangle
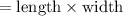 .
.
As per question,
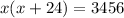
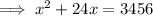
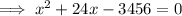
So, the quadratic equation representing the area of the rectangular television screen is
 .
.
Now, to find the dimensions, we need to solve
 .
.

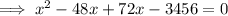
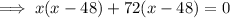
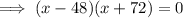
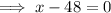 or
or
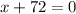
 or
or
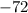
Since,
 is the height of the rectangular television screen, and height cannot be negative. So, height of the television is
is the height of the rectangular television screen, and height cannot be negative. So, height of the television is
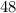 inches, and width of the television screen is
inches, and width of the television screen is
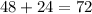 inches.
inches.
Hence, the quadratic equation representing the area of the rectangular television screen is
 .
.
Height of the rectangular television screen
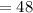 inches, and the width of the rectangular television screen
inches, and the width of the rectangular television screen
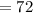 inches.
inches.