Answer:
B. 40
Explanation:
We have been given that segment KN bisects angle JKL.
Since we know that bisects means diving exactly into two equal parts, so measure of angle LKN will be equal to measure of angle JKN.
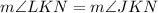
Upon substituting our given information in above equation we will get,
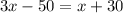
Let us solve for x by combining like terms.
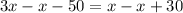
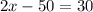
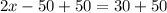
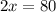
Upon dividing both sides of our equation by 2 we will get,
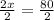
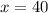
Therefore, the value of x is 40 and option B is the correct choice.