Question

Given the diagram below, if the area of the shaded region is 103 ft2, what are the dimensions of the inside triangle?

Answer 1

Bigger rectangle:

we can see that

length is 3x-2

so,
`L=3x-2`

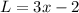
width is x+6

so,
`W=x+6`

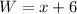
now, we can find area

`A_b=L* W`

`A_b=(3x-2)* (x+6)`

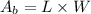
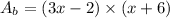
Smaller rectangle:

we can see that

length is 2x

so,
`L=2x`

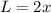
width is x-1

so,
`W=x-1`

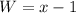
now, we can find area

`A_s=L* W`

`A_s=(2x)* (x-1)`

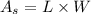
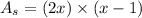
Area of shaded region:

Area of shaded region = area of bigger rectangle - area of smaller rectangle

`A=A_b-A_s`

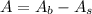
we can plug values

`A=((3x-2)* (x+6))-((2x)* (x-1))`

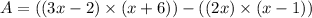
we are given that area as 103 ft^2

so, we can set it equal

`103=((3x-2)* (x+6))-((2x)* (x-1))`

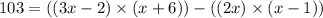
now, we can solve for x

`103=x^2+18x-12`

`x^2+18x-12-103=103-103`

`x^2+18x-115=0`

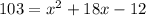
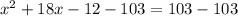
now, we can factor it

`(x-5)(x+23)=0`

`x=5,x=-23`

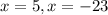
Since, length can never be negative

so,

`x=5`

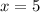
now, we can find dimensions of inner rectangle

Length is

`L=2* 5`

`L=10ft`

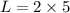
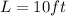
width is

`W=5-1`

`W=4ft`

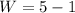
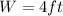
so, dimensions are

`L=10ft`

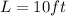
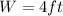`W=4ft`..............Answer