Question

Find the distance from point A to XZ. Round your answer to the nearest tenth. (Explain please)

Answer 1

The distance from point A to the segment XZ is equal the distance between points A and Y.

Why? Because AY is perpendicular to XZ. And this is the shortest distance.

The formula of a distance between two points:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

We have A(3, 0) and Y(0, 1). Substitute:

`d=√((0-3)^2+(1-0)^2)=√((-3)^2+1^2)=√(9+1)=√(10)`

`√(10)\approx3.2`

Answer: d = 3.2

Answer 2

3.2 units.

Explanation:

We have been given an image on coordinate plane. We are asked to find the distance between point A to segment XZ.

We will use distance formula to solve our given problem.

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

Since segment AY is perpendicular to segment XZ, so we will use points A and Y to find distance between point A to segment XZ.

Let point
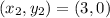`(x_2,y_2)=(3,0)` and
`(x_1,y_1)=(0,1)`.

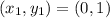Substitute coordinates of both points in distance formula.

`D=√((3-0)^2+(0-1)^2)`

`D=√((3)^2+(-1)^2)`

`D=√(9+1)`

`D=3.16227766`

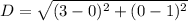
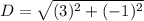
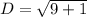
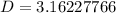
Round to nearest tenth:

`D=3.2`

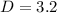
Therefore, the distance from point A to segment XZ will be 3.2 units.