Solution: We are given that females have pulse rates that are normally distributed with a
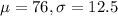
We have to find
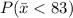
First we need to determine the z score corresponding to
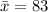
We know that:

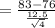
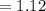
Now, we have to find
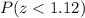
Using the standard normal table, we have:
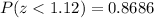
Therefore, if 4 adult females are randomly selected the probability that they have pulse rates with a mean less than 83 beats per minute is 0.8686