Question

The value of computer decreases with its age until it is worth nothing a computer that was purchases new for 0 years is worth 2220 1540 after 6 years problem whats the value after 8 years and what is the linear function V(x)

Answer 1

`V(x) = -(340)/(3)x +2220`

`V(8) = 1313.3`

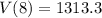
Explanation:

Given

Let x represent years and V represents the value.

So, we have:

`(x_1,v_1) = (0,2220)`

`(x_2,v_2) = (6,1540)`

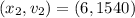
Solving (a): The linear function

First, we calculate the slope (m)

`m = (v_2 - v_1)/(x_2 - x_1)`

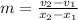
This gives:

`m = (1540-2220)/(6-0)`

`m = (-680)/(6)`

`m = -(340)/(3)`

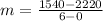
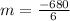
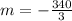
The linear function is calculated using:

`v - v_2 = m(x - x_2)`

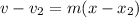
Where:

`(x_2,v_2) = (6,1540)`

`m = -(340)/(3)`

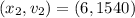
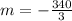
So, we have:

`v - 1540 = -(340)/(3)(x - 6)`

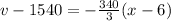
Open bracket

`v - 1540 = -(340)/(3)x +(340)/(3)* 6`

`v - 1540 = -(340)/(3)x +680`

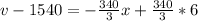
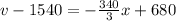
Make v the subject

`v = -(340)/(3)x +680+1540`

`v = -(340)/(3)x +2220`

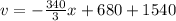
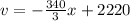
So, the function is:

`V(x) = -(340)/(3)x +2220`

Solving (b): When x = 8

Substitute 8 for x in
`V(x) = -(340)/(3)x +2220`

`V(8) = -(340)/(3)*8 +2220`

`V(8) = -(340*8)/(3) +2220`

`V(8) = -(2720)/(3) +2220`

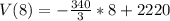
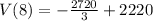
Take LCM

`V(8) = (-2720+2220*3)/(3)`

`V(8) = (-2720+6660)/(3)`

`V(8) = (3940)/(3)`

`V(8) = 1313.3`

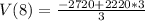
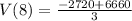
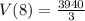
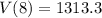
Hence, its value after 8 years is 1313.3