Question

How are half life and radioactive decay related

Answer 1

Answer : Half life and radioactive decay are inversely proportional to each other.

Explanation :

The mathematic relationship between the half-life and radioactive decay :

`N=N_oe^(-\lambda t)` ................(1)

where,

N = number of radioactive atoms at time, t

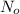`N_o` = number of radioactive atoms at the beginning when time is zero

e = Euler's constant = 2.17828

t = time

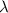`\lambda` = decay rate

when
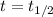`t=t_(1/2)` then the number of radioactive decay become half of the initial decay atom i.e
`N=(N_o)/(2)`.

Now substituting these conditions in above equation (1), we get

`(N_o)/(2)=N_oe^{-\lambda t_(1/2)}`

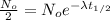
By rearranging the terms, we get

`(1)/(2)=e^{-\lambda t_(1/2)}`

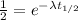
Now taking natural log on both side,

`ln((1)/(2))=-\lambda * t_(1/2)`

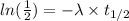
By rearranging the terms, we get

`t_(1/2)=(0.693)/(\lambda)`

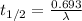
This is the relationship between the half-life and radioactive decay.

Hence, from this we conclude that the Half life and radioactive decay are inversely proportional to each other. That means faster the decay, shorter the half-life.