Question

A fit is rolled 25 times and 12 evens are observed. Calculate and interpret a 95% confidence interval to estimate the true proportion of evens rolled on a die.

Answer 1

95% confidence interval to estimate the true proportion of evens rolled on a die.

(0.197368 , 0.762632)

Step-by-step explanation:

Step-by-step explanation:-

Given A fit is rolled 25 times and 12 evens are observed

proportion
`p = (x)/(n) = (12)/(25) = 0.48`

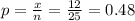
q = 1 - p = 1- 0.48 = 0.52

Level of significance =0.05

`Z_(0.05) = 1.96`

95% confidence interval to estimate the true proportion of evens rolled on a die.

`(p^(-) - Z_(0.05) \sqrt{(p(1-p))/(n) } , p^(-) + Z_(0.05) \sqrt{(p(1-p))/(n) } )`

`(0.48 - 1.96 \sqrt{(0.48(1-0.48))/(12) } , 0.48 + 1.96 \sqrt{(0.48(1-0.48))/(12) } )`

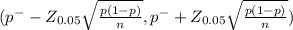
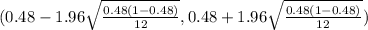
( 0.48 - 1.96 (0.1442 , 0.48 + 1.96(0.1442)

( 0.48 - 0.282632 , 0.48 + 0.282632)

(0.197368 , 0.762632)

Final answer:-

95% confidence interval to estimate the true proportion of evens rolled on a die.

(0.197368 , 0.762632)