Question

A house was haunted by a combined total of 51 ghosts, goblins, and ghouls. On Friday, there were half as many ghosts as there was goblins. On Saturday, two-thirds of the ghouls each became a ghost. On Sunday, 11 of the ghosts each became a goblin, and the ratio of ghouls to goblins became 1:3. If no other changes occurred, how many ghosts are there?

Answer 1

Let x represent the numbers of ghosts on Friday

y represent the numbers of ghouls on Friday

z represent the numbers of goblins on Friday

Their total is 51, so x+y+z= 51

On Friday, there were half as many ghosts as there was goblins

so x = z/2.

Given: On Saturday, two-thirds of the ghouls each became a ghost.

so the number of ghosts on Saturday is
`x+(2)/(3)y`

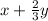
the number of ghouls is
`y - (2)/(3)y=  (1)/(3)y`

Given : On Sunday, 11 of the ghosts each became a goblin, and the ratio of ghouls to goblins became 1:3.

On Sunday, the number of ghosts is
`x+(2)/(3)y-11`

the number of ghouls is 1/3y

and the number of goblins is z+11.

Given : The ratio of ghouls to goblins is 1:3, so ...

`(1)/(3) y : (z+11) = 1:3`

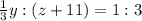
make a fraction and cross multiply it

y = z+ 11

From the relationship we got

x +y +z = 51

`x=(z)/(2)`

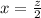
y =z+11

Replace second and third equation in the first equation

`(z)/(2) + z+11 +z = 51`

multiply the whole equation by 2

z +2z +22 +2z = 102

5z + 22 = 102

Subtract both side by 22

5z= 60 ( divide both sides by 5)

z= 16

`x=(z)/(2)`

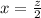
Plug in 16 for z

So x= 8

y =z+11

so y = 16+11= 27

x=8 , y=27 and z=16

The number of ghosts on Friday = 8

the number of ghosts on Saturday is
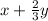`x+(2)/(3)y` = 8 + 18 = 26

the number of ghosts on Sunday is
`x+(2)/(3)y-11`

= 8 + 18 -11=15