We are given rectangle with vertices (6, −3) , (3, −6) , (−1, −2) , and (2, 1) .
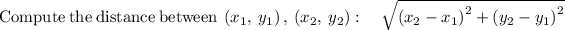
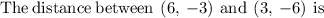

Length of the rectangle is
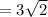 .
.
Width of the rectangle is
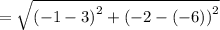
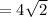
Area of the rectangle = length × width.
Plugging values of length and width in above formula, we get
Area =
 = 12(2) =24 square units.
= 12(2) =24 square units.
Therefore, area of the rectangle is 24 square units.