Question

Given the function f(x) = x^4 + 3x^3 - 2x^2 - 6x - 1, use intermediate theorem to decide which of the following intervals contains at least one zero. Select all that apply.

Answer 1

(a). [-4, -3]

(c). [-2, -1]

(d). [-1, 0]

(f). [1, 2]

Explanation:

The Intermediate Value Theorem states that, for a function f(x) which is continuous in [a, b] also f(a) and f(b) has opposite signs, then there must be a point c lies in interval (a, b) such that f(c) = 0.

we have function: f(x) = x⁴ + 3x³ - 2x² - 6x - 1

(a) [-4, -3]: Calculating

f(-4) = (-4)⁴ + 3(-4)³ - 2(-4)² - 6×-4 - 1 = 55

f(-3) = -1

both has opposite sign so there must be at least one zero lies in the interval [-4, -3]

(b) [-3, -2]

f(-3) = -1

f(-2) = -5

Since both has same sign, Hence no zeros lies in this interval.

(c) [-2, -1]

f(-2) = -5

and f(-1) = 1

Since both has opposite sign hence at least one zeroes lies in this interval.

(d) [-1, 0]

f(-1) = 1

f(0) = -1

Since both has opposite sign hence at least one zeroes lies in this interval.

(e) [0, 1]

f(0) = -1

f(1) = -5

Since both has same sign, Hence no zeros lies in this interval.

(f) [1, 2]

f(1) = -5

f(2) = 19

Since both has opposite sign hence at least one zeroes lies in this interval.

Answer 2

`f(x) = x^4 + 3x^3 - 2x^2 - 6x - 1`

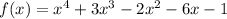
Lets check with every option

(a) [-4,-3]

We plug in -4 for x and -3 for x

`f(-4) = (-4)^4 + 3(-4)^3 - 2(-4)^2 - 6(-4) - 1= 55`

`f(-3) = (-3)^4 + 3(-3)^3 - 2(-3)^2 - 6(-3) - 1= -1`

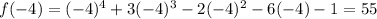
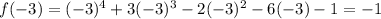
f(-4) is positive and f(-3) is negative. there is some value at x=c on the interval [-4,-3] where f(c)=0. so there exists atleast one zero on this interval.

(b) [-3,-2]

We plug in -3 for x and -2 for x

`f(-3) = (-3)^4 + 3(-3)^3 - 2(-3)^2 - 6(-3) - 1= -1`

`f(-2) = (-2)^4 + 3(-2)^3 - 2(-2)^2 - 6(-2) - 1= -5`

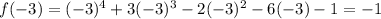
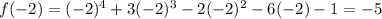
f(-2) is negative and f(-3) is negative. there is no value at x=c on the interval [-3,-2] where f(c)=0.

(c) [-2,-1]

We plug in -2 for x and -1 for x

`f(-2) = (-2)^4 + 3(-2)^3 - 2(-2)^2 - 6(-2) - 1= -5`

`f(-1) = (-1)^4 + 3(-1)^3 - 2(-1)^2 - 6(-1) - 1= 1`

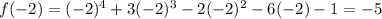
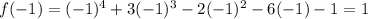
f(-2) is negative and f(-1) is positive. there is some value at x=c on the interval [-2,-1] where f(c)=0. so there exists atleast one zero on this interval.

(d) [-1,0]

We plug in -1 for x and 0 for x

`f(-1) = (-1)^4 + 3(-1)^3 - 2(-1)^2 - 6(-1) - 1= 1`

`f(0) = (0)^4 + 3(0)^3 - 2(0)^2 - 6(0) - 1= -1`

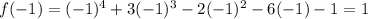
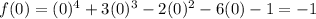
f(-1) is positive and f(0) is negative. there is some value at x=c on the interval [-1,0] where f(c)=0. so there exists atleast one zero on this interval.

(e) [0,1]

We plug in 0 for x and 1 for x

`f(0) = (0)^4 + 3(0)^3 - 2(0)^2 - 6(0) - 1= -1`

`f(1) = (1)^4 + 3(1)^3 - 2(1)^2 - 6(1) - 1= -5`

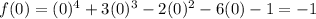
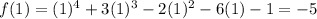
f(0) is negative and f(1) is negative. there is no value at x=c on the interval [0,1] where f(c)=0.

(f) [1,2]

We plug in 1 for x and 2 for x

`f(1) = (1)^4 + 3(1)^3 - 2(1)^2 - 6(1) - 1= -5`

`f(2) = (2)^4 + 3(2)^3 - 2(2)^2 - 6(2) - 1= 19`

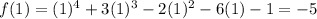
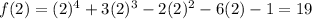
f(-4) is positive and f(-3) is negative. there is some value at x=c on the interval [-4,-3] where f(c)=0. so there exists atleast one zero on this interval.

so answers are (a) [-4,-3], (c) [-2,-1], (d) [-1,0], (f) [1,2]