Question

Use the rational zero theorem to create a list of all possible rational zeroes of the function f(x) = 14x^7 - 4x^2 + 2

Answer 1

`\pm 1, \pm 2 \pm (1)/(2),\pm (1)/(7),\pm (1)/(14), \pm (2)/(7)`

Explanation:

By the rational root theorem or rational zero theorem,

The possible;e solutions of a polynomial function is,

`\pm(\frac{\text{factors of the constant term}}{\text{Factors of the leading coefficient}})`

Here, the given function,

`f(x) = 14x^7 - 4x^2 + 2`

Constant term = 2 and Leading coefficient = 14,

Factors of 2 = 1, 2,

Factors of 14 = 1, 2, 7, 14

Hence, the possible roots of the function,

`\pm((1, 2)/(1, 2, 7, 14))`

`=\pm 1, \pm 2, \pm (1)/(2),\pm (1)/(7),\pm (1)/(14),\pm (2)/(7)`

Answer 2

`f(x) = 14x^7 - 4x^2 + 2`

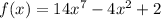
Use the rational zero theorem

In rational zero theorem, the rational zeros of the form +-p/q

where p is the factors of constant

and q is the factors of leading coefficient

`f(x) = 14x^7 - 4x^2 + 2`

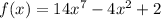
In our f(x), constant is 2 and leading coefficient is 14

Factors of 2 are 1, 2

Factors of 14 are 1,2, 7, 14

Rational zeros of the form +-p/q are

`+-(1,2)/(1,2,7,14)`

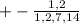
Now we separate the factors

`+-(1)/(1), +-(1)/(2), +-(1)/(7), +-(1)/(14),+-(2)/(1), +-(2)/(2), +-(2)/(7), +-(2)/(14)`

`+-1, +-(1)/(2), +-(1)/(7), +-(1)/(14),+-2, +-1 , +-(2)/(7), +-(1)/(2)`

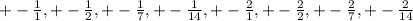
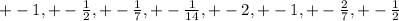
We ignore the zeros that are repeating

`+-1, +-2, +-(1)/(2), +-(1)/(7), +-(1)/(14), +-(2)/(7)`

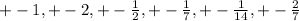
Option A is correct