Question

Use the identity x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx) to determine the value of the sum of three integers given: the sum of their squares is 110, the sum of their cubes is 684, the product of the three integers is 210, and the sum of any two products (xy+yz+zx) is 107. Enter your answer as an integer, like this: 42

Answer 1

ffn

`x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)`

`x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-(xy+yz+zx))`

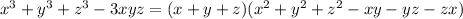
the sum of their squares is 110, So
`x^2+y^2 + z^2= 110`

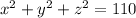
the sum of their cubes is 684, so
`x^3+y^3 + z^3= 684`

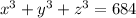
the product of the three integers is 210, so xyz= 210

the sum of any two products (xy+yz+zx) is 107

Now we plug in all the values in the identity

`x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-(xy+yz+zx))`

684 - 3(210) = (x+y+z)(110-107)

684 - 630 = (x+y+z)(3)

54 = 3(x+y+z)

Divide by 3 on both sides

18 = x+y+z

the value of the sum of three integers is 18