Question

Please help me
Show your work

Answer 1

ANSWER TO PART A

The given triangle has vertices
`J(-4,1), K(-4,-2),L(-3,-1)`

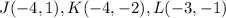
The mapping for rotation through
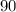`90\degree` counterclockwise has the mapping

`(x,y)\rightarrow (-y,x)`

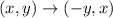
Therefore

`J(-4,1)\rightarrow J'(-1,-4)`

`K(-4,-2)\rightarrow K'(2,-4)`

`L(-3,-1)\rightarrow L'(1,-3)`

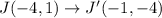
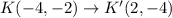
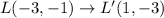
We plot all this point and connect them with straight lines.

ANSWER TO PART B

For a reflection across the y-axis we negate the x coordinates.

The mapping is

`(x,y)\rightarrow (-x,y)`

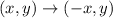
Therefore

`J(-4,1)\rightarrow J''(4,1)`

`K(-4,-2)\rightarrow K''(4,-2)`

`L(-3,-1)\rightarrow L''(3,-1)`

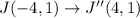
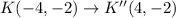
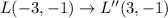
We plot all this point and connect them with straight lines.

See graph in attachment