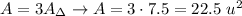Question

Find the area of the polygon. show your work

Answer 1

Look at the picture.

We have the triangle and the parallelogram.

The formula of an area of a triangle

`A_T=(bh)/(2)`

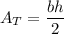
We have b = 5 and h = 3. Substitute:

`A_T=(5\cdot3)/(2)=(15)/(2)=7.5`

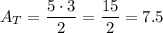
The fromula of an area of a parallelogram:

`A_P=bh`

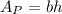
We have b = 5 and h = 3. Substitute:

`A_P=5\cdot3=15`

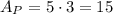
The area of polygon:

`A=A_T+A_P\to A=7.5+15=22.5\ u^2`

--------------------------------------------------

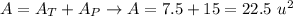
Other method. (look at the second picture).

We have the three congruent triangles. The area of the polygon is equal three times the area of a one triangle.

`A_\Delta=(bh)/(2)`

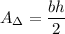
b = 5, h = 3. Subsitute.

`A_\Delta=(5\cdot3)/(2)=(15)/(2)=7.5`

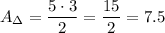
The area of the polygon:

`A=3A_\Delta\to A=3\cdot7.5=22.5\ u^2`