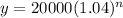Question

a team of scientists estimate the current number of butterflies In A park to be 20 thousand. the butterfly population is expected to increase at a rate of 4% per year. which equation models the number of butterflies, in thousands, in the park after n years?

Answer 1

Current number of butterflies in the park = 20 thousand.

Rate of increase of butterfly population = 4% = 0.04

The population of butterfly after 1 year = 20+0.04*20 = 20*1.04

The population of butterfly after 2 years = 20*1.04 + 20*1.04*0.04 = 20*1.04*1.04

The population of butterfly after 3 years = 20*1.04*1.04 + 20*1.04*1.04*0.04 = 20*1.04*1.04*1.04

So, population of butterfly after n years = 20*(1.04*1.04*1.04* .... n times)

Answer 2

`y=20000(1.04)^n`

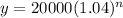
Explanation:

This will be an exponential growth equation, of the form

`y=a(1+r)^x`,

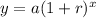where a represents the initial population, r represents the rate of growth per year, and x represents the number of years.

The initial population is 20,000. This goes in place of a.

The rate of growth is 4%. 4% = 4/100 = 0.04; this goes in place of r.

We are using n to represent years instead of x.

This gives us

`y=20000(1+0.04)^n`

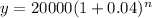
Adding in parentheses gives us

`y=20000(1.04)^n`