Question:
What is the perimeter of the path, in miles?
Answer:
35 miles
Explanation:
Given
Let the corners be ABCD
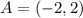
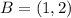
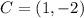
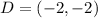
First, we calculate the perimeter of the corners in units.
This is done by calculating the distance between the corners.
Distance is calculated as:

For AB:

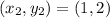
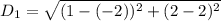
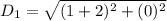
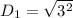
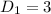
For BC
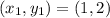
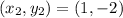
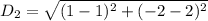
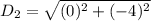
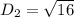

For CD:
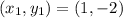

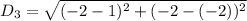
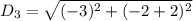
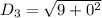
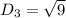
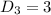
For DA

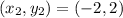
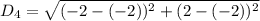
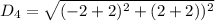
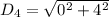

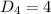
The perimeter P in units is:
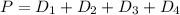
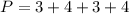
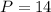
Given that:
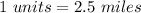
Multiply both sides by 14
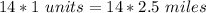
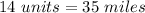
Hence, the perimeter is 35 miles