Answer: IV, positive,
 , - sec
, - sec
 ,
,
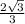
Explanation:
a) Look at the Unit Circle to see that
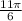 = 330°, which is located in Quadrant IV.
= 330°, which is located in Quadrant IV.
b) The coordinate (cos θ, sin θ) for
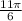 is:
is:
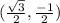
sec =
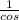 =
=
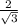 which is positive
which is positive
c) Since the given angle is in Quadrant IV, which is closest to the x-axis at 360° = 2π, the reference angle can be found by subtracting the given angle
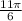 from 2π:
from 2π:
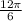 -
-
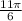 =
=

d) the reference angle is below the x-axis so the given angle is equal to the negative of the reference angle: - sec
 .
.
e) sec
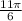 =
=
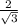 =
=
 =
=
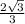
***************************************************************************************
Answer:
 , IV,
, IV,
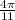
Explanation:
2π is one rotation. 2π =

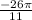 +
+
 =
=

 +
+
 =
=

Convert the radians into degrees to see which Quadrant it is in by setting up the proportion and cross multiplying:
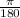 =
=
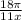
π(11x) = (180)18π
x =
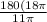
x = 295° which lies in Quadrant IV
Since the given angle is in Quadrant IV, which is closest to the x-axis at 360° = 2π, the reference angle can be found by subtracting the angle of least nonegative value
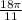 from 2π:
from 2π:
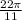 -
-
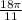 =
=
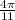
***************************************************************************************
Answer:
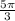 , IV,
, IV,
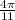 ,
,

Explanation:
2π is one rotation. 2π =
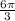
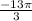 +
+
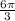 =
=
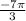
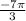 +
+
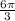 =
=

 +
+
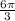 =
=
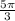
This is on the Unit Circle at 300°, which is located in Quadrant IV
Since the given angle is in Quadrant IV, which is closest to the x-axis at 360° = 2π, the reference angle can be found by subtracting the angle of least nonegative value
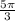 from 2π:
from 2π:
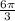 -
-
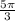 =
=
