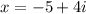ANSWER:
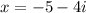 or
or
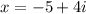
Step-by-step explanation:
The equation given to us is
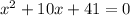 .
.
One way to solve this equation is to use the quadratic formula;
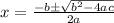
When we compare
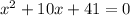 to the general quadratic equation
to the general quadratic equation
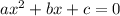 .
.
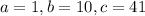
When we substitute these values in to the formula, we obtain;
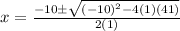
We evaluate to obtain;
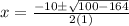
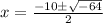
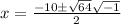
Note that in complex numbers;
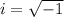
This implies that;
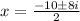
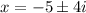
When we split the plus or minus sign we get;
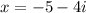
or