Question

Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.

Five times the sum of the digits of a two-digit number is 13 less than the original number. If you reverse the digits in the two-digit number, four times the sum of its two digits is 21 less than the reversed two-digit number.

(Hint: You can use variables to represent the digits of a number. If a two-digit number has the digit x in tens place and y in one’s place, the number will be 10x + y. Reversing the order of the digits will change their place value and the reversed number will 10y + x.)

The difference of the original two-digit number and the number with reversed digits is

Answer 1

Let the number be = 10x+y

Let the reverse number be = 10y+x

Equations are:

`5(x+y)=10x+y-13`

`4(x+y)=10y+x-21`

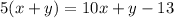
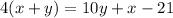
Solving and rearranging we get

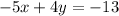`-5x+4y=-13` .... (1)

`3x-6y=-21` ...... (2)

Multiplying equation (1) by 3 and equation (2) by 5 to get same x

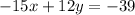`-15x+12y=-39` .... (3)

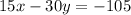`15x-30y=-105` .... (4)

Adding (3) and (4), we get

`-18y=-144`

`y=8`

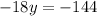
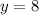
Solving for x,
`-15x+12(8)=-39`

`-15x+96=-39`

`-15x=-135`

`x=9`

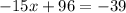
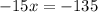
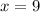
Now, x=9 and y=8

So number is 10x+y

= 10(9)+8 =90+8= 98

And reverse number is 89.

So difference of the original and reverse digits is = 98-89= 9