Answer:
![\sqrt[3]{2}](https://img.qammunity.org/2019/formulas/mathematics/college/k5z835vc617l7man8yhifq74j190yt7qac.png)
Explanation:
If the complex number is given in the form of ( a+bi)
Then absolute value of the complex number will be =
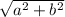
Now the given complex number is (
![-4 \sqrt[-i]{2}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/2wrwluysfktqt49o0hq0gd0ro2cdd5pz0j.png)
So in this number a = ( -4 ) and b =
![\sqrt[-]{2}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/tldeycdjsb9modqg2s8vee9y0cqpp15wdh.png)
Therefore, absolute value will be =
![\sqrt{(-4)^(2)+(\sqrt[-]{2})^(2)}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/ombjjpuaj27o8ftp0sy1pavz0apsrus2q8.png)
=
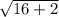
=
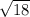
=
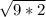
=
![\sqrt[3]{2}](https://img.qammunity.org/2019/formulas/mathematics/college/k5z835vc617l7man8yhifq74j190yt7qac.png)
So absolute value will be
![\sqrt[3]{2}](https://img.qammunity.org/2019/formulas/mathematics/college/k5z835vc617l7man8yhifq74j190yt7qac.png) .
.