Question

After being dropped from a platform, a ball bounces several times. The graph shows the height of the ball after each bounce.

What does the end behavior for x increasing without bound represent?




The end behavior for x decreasing without bound is meaningless in this situation.

The height of the platform is unknown.

The ball will never stop bouncing.

The height of each bounce will approach 0 m.

Answer 1

answer is C

Explanation:

it is wednesday my dudes

Answer 2

End behavior for increasing x represents that the height of each bounce will approach 0.

Solution-

From the graph the exponential equation is,

`y=100e^((-0.35x))`

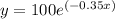
From the properties of negative exponential function properties, as x increases, the value of y decreases.

So, in this case, as x or number of bounce increases, y or the height of bounce decreases. And eventually the value becomes zero.

Therefore, end behavior for increasing x represents that the height of each bounce will approach 0.