Question

Which system of linear inequalities is graphed?

{y>2x+1x+y<−2
{y≥2x+1x+y≤−2
{y<2x+1x+y>−2
{y≤2x+1x+y≥−2

Answer 1

The solution of a linear inequality is the ordered pair that is a solution to all inequalities in the system and the graph of the linear inequality is the graph of all solutions of the system. Graph one line at the time in the same coordinate plane and shade the half-plane that satisfies the inequality.

y<2x+1x+y>−2

Answer 2

y>2x+1; x+y<−2

Explanation:

Since, dotted line represents the inequality with sign '<' or '>',

Thus, y≥2x+1; x+y≤−2 and y≤2x+1 ; x+y≥−2 can not be the system of equations,

Now, by the given graph,

The one of the related equations passes through (0, -2) and (-2, 0)

So, the equation of the related equation,

`y+2=(0+2)/(-2-0)(x+0)`

`y+2=-1x`

`x+y = -2`

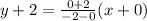
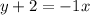
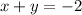
∵ Shaded region of this line does not contain the origin,

Thus, the inequality would be,

`x+y < -2`

Also, other of the related equations passes through (0, 1) and (-1, -1)

So, the equation of the related equation,

`y-1=(-1-1)/(-1)(x+0)`

`y-1=2x`

`y= 2x +1`

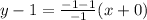
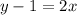
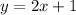
∵ Shaded region of this line does not contain the origin,

Thus, the inequality would be,

y > 2x + 1

Hence, the required system would be,

y>2x+1; x+y<−2