Given:
Present number of trees = 2.5 billions
Rate of decrease = 0.5% per month
To find:
The expression that represents how many trees will be left in 10 years?
Solution:
Exponential decay model:
 ...(i)
...(i)
where, a is initial value, r is decreasing rate and t is time period.
We have,
a = 2.5 billions
r = 0.5% = 0.005 per month
t = 10 years = 120 months [1 year = 12 months]
Putting a=2.5, r=0.005 and t=120 in (i), we get
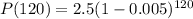
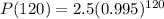
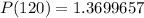
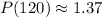
Therefore, the required expression is
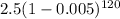 and the remaining trees after 10 years is about 1.37 billions.
and the remaining trees after 10 years is about 1.37 billions.