Answer:
Proved
Explanation:
Solving (a):
Let the numbers be:
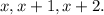
Their sum is:
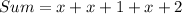
Collect Like Terms
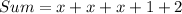
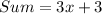
Divide sum by 3.
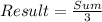
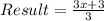
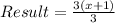
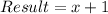
Hence, this is true because there is no fractional part after the division
Solving (b):
Let the numbers be:
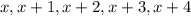
Their sum is:
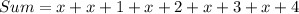
Collect Like Terms

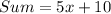
Divide sum by 5.
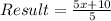

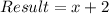
Hence, this is true because there is no fractional part after the division
Solving (c):
Let the numbers be:
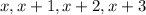
Their sum is:
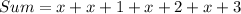
Collect Like Terms
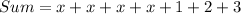
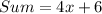
Divide sum by 4.

Split
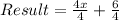
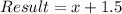
The 1.5 means that the sum can not be divisible by 4