Given:
The Benjamin's distance from City A, t hours after leaving his house is
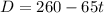
To find:
The slope of the equation and what is its interpretation in the context of the problem?
Solution:
The slope intercept form of a line is

where, m (coefficient of variable x) is slope and b is y-intercept.
We have, the equation
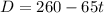
It is a linear equation and the coefficient of variable t is -65. So, the slope of the equation -65.
It means, the Benjamin's distance from City A is decreases at the rate of 65 units per hour or we can say the speed of Benjamin is 65 units per hour.
Therefore, slope of the equation -65. It means, Benjamin's distance from City A is decreases at the rate of 65 units per hour.