Answer-
The value of y is
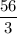 when x=7 and z=4.
when x=7 and z=4.
Solution-
As given in the question, y is directly proportional to x, so
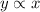 -----------------1
-----------------1
And also y is directly proportional to z, so
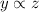 -----------------2
-----------------2
Combining equation 1 and 2,
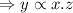
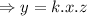
Where,
k = proportionality constant
When x=6 and z=1, y=4. Putting theses values,
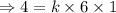
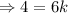

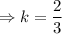
Now, we have to find the value of y, when x=7 and z=4

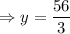
Therefore, the value of y is
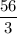 when x=7 and z=4.
when x=7 and z=4.