Answer : option 2,4 and 5 are true statements

We have 6p and 2p^2 in the denominator
Least common denominator LCD = 6p^2
Now we need to make the denominators same

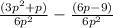
So first fraction becomes
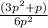
We find the difference by subtracting the numerators
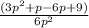
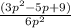
The resulting is a rational expression
So option 2, 4 and 5 are true statements