Answer:
11.58 years
6.82 years
Explanation:
Compound interest can be represented as:
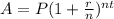 where P = initial amount, r=interest rate, n=compounds in each time unit, t = time (usually years)
where P = initial amount, r=interest rate, n=compounds in each time unit, t = time (usually years)
If you think about it the:
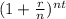 represents the overall interest being applied to the principal amount.
represents the overall interest being applied to the principal amount.
This would have to be equal to 2, for it to be doubled, so let's set that equal to 2
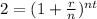
Now let's solve for "t", first let's take the log of both sides
![log(2)=log([1+(r)/(n)]^(nt))](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/itji9u1qbj3ueu0am1iu.png)
Now let's use log properties, specifically the exponent one to rewrite
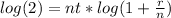
Now divide both sides by the log(1 + r/n) and n

Our "n" is going to be the same for both equations, 12 since it's compounded monthly
The interest will be a bit different, but in the first case it will be 6% which is 0.06
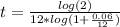
simplifying this we get

Rounding this we get:
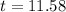
Now let's do this to the other equation:
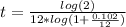
simplifying this we get:

approximately 6.82