Answer:
The equation that represents the equation of the parabola is:
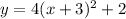
Explanation:
We know that the general equation of the parabola with vertex at (h,k) is represented with the help of the equation:
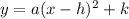
where a is a constant and if a>0 then the parabola is open upward.
and if a<0 then the parabola is open downward.
Here we have the vertex of the parabola at (-3,2)
and a=4 in each of the options.
i.e. we have: h=-3 and k=2
Hence, the equation of the parabola is:
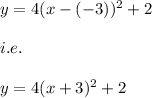
The correct option is:
Option: B