Answer : -4.00
what is the value of
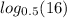
We use log property to find the value
16 = 2*2*2*2 = 2^4
So we replace 16 by 2^4
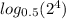
As per log property we move exponent before log
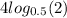
0.5 can be written as 1/2 . 1/2 can be written as 2^-1
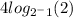
Now we apply change of base formula
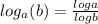
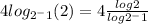
Move the exponent -1 before log
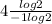
log 2 will get cancelled

-4
-4.00 is the final answer