Question

Which key features can you identify from the following equation? Provide enough information to describe the appearance and behavior of the graph.

f(x)= -6 Radical x-4 + 8 ( + 8 is on outside of radical )

I know the 8 is the y-intercept but got confused on how to describe the function

Answer 1

Plato Answer:The equation reveals that the vertex, or starting point, of this square root function is at (4,8). Because the domain is x ≥ 4, the graph is defined only for x-values to the right of (4,8). To the left of (4,8), the graph is undefined. The coefficient of -6 means the graph will change at a faster rate than the parent graph. The negative sign indicates the function is decreasing on its domain—as x approaches positive infinity, f(x) approaches negative infinity.

Explanation:

Answer 2

Given the function
`f(x)=-6√(x-4)+8.`

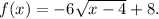
1. The domain of the function (possible values for x) is:

`x-4\ge 0,\\ \\x\ge 4.`

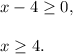
2. The range of the function (possible values for y) is:

`y=f(x)\le 8.`

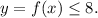
3. x-intercept is when y=0, then

`0=-6√(x-4)+8,\\ \\√(x-4)=(8)/(6)=(4)/(3),\\ \\x-4=(16)/(9),\\ \\x=4+(16)/(9)=(52)/(9)\approx 5.778.`

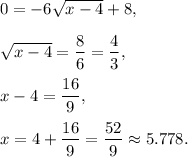
Therefore, x-intercept is at point
`\left(5(7)/(9),0\right).`

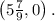
4. There are no y-intercepts.

5. The graph of the function is decreasing (see attached diagram)